AI活用における経済変数の変化シミュレーション

AI活用による影響をマクロ経済に簡単に当てはめて計算してみた。
経済学で、「コブ・ダグラス型」生産関数という生産量を分解して表す方法があるが、それをもとに、AI活用でどの部分に影響して結果として生産量がどうなるのかをシミュレーションした。
コブ・ダグラス型生産関数:
Y = A ⋅ K ^ α ⋅ L ^ β
※変数の意味
・Y:生産量
・A:全要素生産性
・K:資本投入量
・α:資本弾力性 (資本投入量を1%増やしたときに生産量が何%増えるか)
・L:労働投入量
・β:労働弾力性 (労働投入量を1%増やしたときに生産量が何%増えるか)
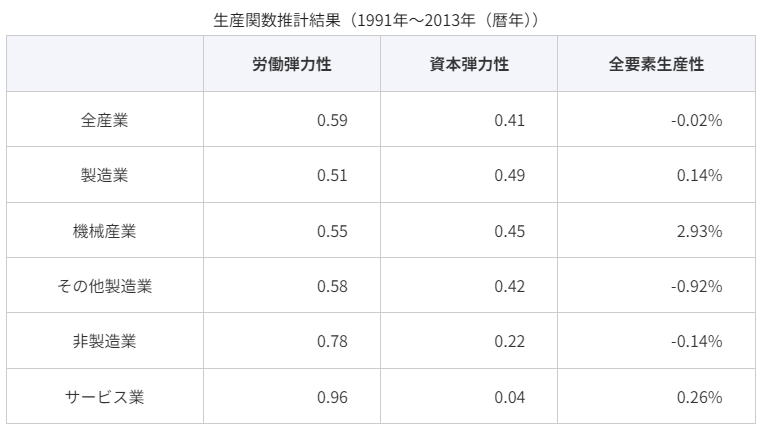
※シミュレーションの元の数値となるαとβは、1991年~2013年の生産関数推計結果から引用。

シミュレーション①:
労働投入量・資本投入量が一定のもとで労働弾力性の向上による生産量の変化
→
シミュレーションの結果、労働弾力性の増加によって、
・0.05ずつの増加で約26%生産量増加
・0.10ずつの増加で約58%生産量増加
など、労働投入の効率性について飛躍的に上昇することがわかる。
シミュレーション②:
資本投入量が一定、労働投入量が減少するもとで労働弾力性の向上による生産量の変化
→
シミュレーションの結果、労働投入量が1%ずつ減少していっても、労働弾力性を増加させることで生産量は数倍に増加させられることがわかる。
シミュレーション③:
資本投入量が一定、労働投入量が元の半分のもとで、労働弾力性が飛躍的に向上する場合における生産量の変化
→
人口が減少した先の長期的な生産構造の現実的なものとしてシミュレートしています。現実的ではないと主張する人もいるが、私個人としてはメチャクチャ現実的な生産構造だと考えている。逆に、これ以外の世界線を想像しづらい。
シミュレーションの結果、労働弾力性の飛躍的な向上によって、生産量は元の数百~数千倍になっている。
今回、資本投入量と資本弾力性については一定としたが、そこの変化によるシミュレーション次第ではAI活用の効果はさらに飛躍的になる可能性がある。また、コブ・ダグラス型生産関数では「規模に対して収穫一定」、つまり資本弾力性と労働弾力性の合計値が1であるということを置くことも多いが、AI活用によって労働弾力性が増加する分、資本弾力性が下がることは基本的に考えられないため、資本弾力性と労働弾力性の合計値が1を超えていくこととした。
シミュレーション③が最も現実的にあり得るものであると記載したが、前提として、マクロ全体でどんな国にも(日本にも)当てはめられるかと言うと、それこそAI活用次第だなと考えている。より現実的に広範囲に一般的なシミュレーションを当てはめやすいという意味では、経済全体というマクロではなく、ミクロでの企業ごとの単位で見たり1人単位で見たりしてAI活用することのほうがイメージしやすいかなと思う。
定量的にシミュレートしたが、定性的に表現すれば、「わざわざ労働を需要するのだから、生産性の高い人や生産性の高い仕組みのなかで労働でレバレッジできる人しか需要しない」世界線が来ているということ。特に自分を含めたホワイトワーカー。
めっちゃ楽しみ&楽しい。
※シミュレーションのExcelは下記。feel free to use.
